Computation of Volume

 

Computationof Volume

·       In many civil engineering projects, earth work involve the excavation, removal and dumping of earth, therefore it is required to make good estimate of volume of earth work.

·       Volume computation are also required to determine the capacity of reservoirs.

·       The volume of the earth work is calculated by

                          I.          The Trapezoidal rule

                        II.          The Prisimoidal Rule.

Example:

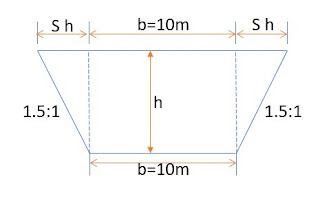
An embankment of width 10m and side slope 1.5:1 is required to be made on a ground which is level in a direction traverse to centre line . The central height at 20m intervals are as follows 08,1.2,2.25,2.6,1.9,1.4 and 0.9

Calculate the volume of earth work according to

      I.          The trapezoidal rule

    II.          The Prisimoidal rule

Solution:

Here b=10m, S=1.5, interval=20m

The cross-sectional area is calculated by equation

Area= (b+sh) h

Δ₁=(10+1.5 x0.8)0.8=8.96m²

Δ₂= (10+1.5 x1.2)1.2=14.16m²

Δ₃=(10+1.5 x2.25)2.25=30.09m²

Δ₄=(10+1.5 x2.6)2.6=36.14m²

Δ₅=(10+1.5 x1.9)1.9=24.42m²

Δ₆=(10+1.5 x1.4)1.4=16.94m²

Δ₇=(10+1.5 x0.9)0.9=10.22m²

Volume From Spot Levels:

·       In this method, the field work consists in dividing the area in to a number of squares, rectangles (or) triangles and measuring the levels of their corners before and after the construction.

·       Thus the depth of excavation (or) height of filling at every corner is known

·       Let us assume that the four corners of any one square (or) rectangle are at different elevations but lie in the same inclined plane.

·       The rectangle abcd represents the horizontal projection of the upper inclined base of the prism and also the lower horizontal base.

·       Let us consider the rectangle abcd, ha, hb, hc , and hd represent the depth of excavation of the four corners , the volume of the right truncated prism will be given by